Ramen的算法笔记.1
这个系列自从出了个预告,然后就什么都没有了。
哎,这段时间好划啊,什么都没研究进去,只能吃吃老本了。
最近也是忙的要死,什么技术性文章都没写,是时候动笔了。
(DDM会复活的,相信我!!!
对了,这篇文章开始结构要发生改变,预告里面那个结构太智障不实用了。
Ramen的算法笔记.1 并查集
什么是并查集?说这个问题前,我们先想一个情景:
我有100位好朋友,现在我要举办一场Party!Whoo!
在我的这些朋友中,有一些人相互认识,比如A认识C,C又认识E,然后W认识X……
认识的人坐一起那当然更爽了!比如A、C、E坐一桌,W和X坐一桌……
现在我想问你,我最少需要多少张桌子?
怎么样,是否有点清晰了?并查集解决的就是这样的问题。
简单来说,就是把相似的划分进一组,最后问问你有几组的问题。
这个问题我们可以想象网络,每两台的连接起来的机器分进一组,那么我们很容易就能计算出当前有多少组机器互联了,假如我们新增加一组机器可以让三组互联,那么让它们全部互联还需要加机组机器这样的问题。存储这种关系并返回查询结果的数据结构就是并查集了。
1.定义与API
1.1定义
并查集,Union-Find Set,也叫用于不相交集合的数据结构,Disjoint-Set Data Structure。
在计算机科学中,并查集是一种树型的数据结构,其保持着用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。有一个联合-查找算法(union-find algorithm)定义了两个操作用于此数据结构。
——维基百科
那么并查集的最终用途,就是用于对一组不相交集合进行合并操作,并从此查询,获得关于元素的信息。在这个过程中,我们把元素抽象为一个个触点,而每一个集合里面的元素都是联通的,所联通的两个触点间的路径被我们称为联通分量。
显然,我们把集合抽象为了一个无向图。
这是一个用树去处理图的数据结构。想到什么了吗?对,最小生成树。我们会在最小生成树这一节用到并查集。
1.2 API
下面是并查集的API接口。
接口的描述形式采用《算法(第4版)》的形式。(橙书好橙书棒,橙书你买不了吃亏买不了上当~
| |
| 返回值 | API | 解释 |
|---|---|---|
UF(int n) | 构造一个有n个触点的并查集 | |
~UF() | 析构此并查集 | |
void | Union(int p, int q) | 添加触点p到触点q的联通分量 |
int | find(int p) | 返回触点p的所在分量的标识符(代表元素、根触点) |
bool | connected(int p, int q) | 查询是否触点p与触点q在一个联通分量里面 |
int | getCount() | 返回联通分量的数量 |
2.算法细节
从API定义我们能看到,并查集所实现的操作十分简单,而且极为清晰。
首先我们来想,怎么存这个图。很显而易见的是,这个图没有权值(也可以说权值均为1),所以我们并不需要邻接矩阵或者邻接链表。这里一维数组就足够解决一切问题。显而易见的是,联通分量最初为n个,因为没有任何触点此时是联通的。
接下来的问题是,怎么表示两个触点在一个联通分量里面?
第一种做法很简单,如果二者在同一个联通分量里面,说明二者具有相同的性质,那就让这二者都指向其中一个就行了,比如1和8在一个联通分量里面,那么1和8的数组数据要么都是1要么都是8不就结束了?
这种方法我们能证明在$O(1)$的时间内就能把两个触点添加到同一个联通分量里面。但是我们要查询呢?很显然,很麻烦,最坏的情况是,查询其中一个元素遍历了$n/2$的数组,而另一个元素也需要遍历$n/2$次数组,这样算法复杂度很大。进一步研究表示,假如我们添加了所有联通分量,也就是最后只剩一个联通分量,那我们最终需要访问$(N+3)(N-1)$次数组,也就是$O(N^2)$的复杂度。现实生活中这样的算法实际上无法使用,因为并查集一般需要处理的问题大概在百万级别,这样的复杂度实在是太高了。
第二种做法就显得复杂但是速度更快。我们这么想,一开始我们让所有触点指向自己,也就是说所有触点的根触点是它们自己。之后我们归并两个触点的时候,我们只需要让它们指向同一个根触点就行。
举例来说,一开始是1和8,那么我们让1仍旧指向自身,然后让8指向1。后来我们又需要添加8和3,那么只需要让3也指向1,此时我们查询8和3,能查到这二者根触点是一个,这二者就在一个联通分量里面。此时根触点就是分量的标识符。
眼熟吗?对,这就是一棵树。
弄懂了这里,我们就可以开始考虑实现了。
3.实现
实现阶段,我们有以下问题需要考虑。
多少个触点?
我们一共有
n个触点,所以我们需要一个n大小的数组。动态内存分配即可。1int *id = new int[n];这个时候要注意析构:
1delete[] id;初始化?
初始化让所有触点指向自己即可:
1 2for (int i = 0; i < N; i++) id[i] = i;怎么查找?
由上面的讨论我们知道,到后面会出现树挂到根触点的情况,所以我们不能只是简单找到一个点就结束了。根据我们的讨论,我们知道一个循环即可,退出条件是触点指向自己。
1 2 3 4 5 6int find(int p) { while (p != id[p]) p = id[p]; return p; }归并操作?
归并操作就简单许多,我们让其指向一个统一的根触点即可。
1 2 3 4 5 6 7 8 9 10 11 12void Union(int p, int q) { int pRoot = find(p); int qRoot = find(q); if (pRoot == qRoot) return; id[pRoot] = qRoot; // id[qRoot] = pRoot is valid too. count--; }
这些问题解决了,实现起来就简单了,下面是完整实现:
| |
4.优化
优化这个板块可能出现可能不出现,取决于怎么讲和这个数据结构有没有优化。
这个算法比起上一个要快,至少在平均状况下。但是在最复杂的情况下,它的复杂度仍然能到达$O(N^2)$。这是因为当这个树是一棵单边树,也就是所有节点都连接在同一侧的时候,我们的整个寻找过程跟第一种情况一样。
那么我们怎么优化呢?再优化存储结构行不通了,接下来让我们分别看看合并和查询操作。
4.1合并操作的优化——按秩合并
首先解决一个问题,什么是秩?我们可以简单的理解为树的深度。按秩合并是一种什么优化呢?我们考察这个例子:
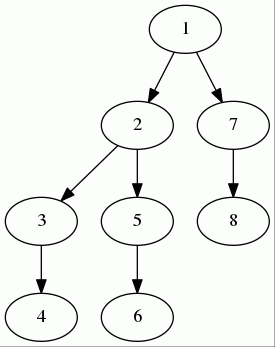

你会怎么合并?
根据刚才的讨论,我们应该尽量减少树的深度,所以显而易见的是,我们应该把第二棵树链接到第一棵树上。
4.2查询操作的优化——路径压缩
继续考虑第一张图:

想一个问题:当我们查询4的时候,我们最终肯定要查询到根触点1。这也就是说,4这个联通分量的标识符就是1。那么我们能不能这么做,直接把4挂到1下面,不用再经过3和2?当然可以!本着“前人栽树后人乘凉”的原则,这个操作就让查询来实现——也就是说,当我们查询一个节点的时候,我们索性把一条路都挂到根触点上。这样操作之后,图一就变成如下这个样子:
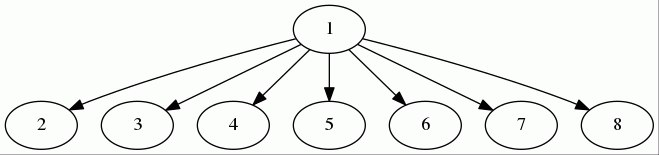
最理想的情况下,这棵树的深度就是2,一个根触点连接了所有触点。
4.3实现
代码实现起来就很简单了:
按秩合并
首先,我们需要新建一个表示秩的数组并将其全部初始化为1:
1 2 3int *sz = new int[n]; for(int i = 0; i < n; i++) sz[i] = 1;当然,析构也需要这一句:
1delete[] sz;其次,在合并过程中,我们需要如下判断:
1 2 3 4 5 6 7 8 9 10if (sz[pRoot] < sz[qRoot]) { id[pRoot] = qRoot; sz[qRoot] += sz[pRoot]; } else { id[qRoot] = pRoot; sz[pRoot] += sz[qRoot]; }这就完成啦!
这里我们做了一层判断,如果左树深度小于右树,就把左树挂到右树上并更新秩,否则就反过来。
路径压缩
路径压缩只需要在查询操作中添加两个辅助暂存变量并再度遍历即可:
1 2 3 4 5 6 7 8 9 10int k = p, j; /* Original Code */ while (k != p) { j = id[k]; id[k] = p; k = j; }while循环的退出条件是我们已经来到了根触点。在之前的遍历中,我们已经把当前根触点存到了p中,所以简单判断k!=p即可。接下来的第一行,我们把当前触点的前一个触点暂存到j中,然后下一行把当前触点的根触点更新为p,最后一行修改搜索索引k。短短三行代码就解决了!
下面给出完整代码实现:
| |
这就是全部了。
5.讨论
能否再进一步优化?
经过按秩合并的优化,我们的复杂度变为$O(NlgN)$,已经很不错了。而当我们进行了路径压缩优化后,这个复杂度更加变成了难以置信的十分接近于$O(N)$(十分接近于但是并没有达到)。而在研究之后,我们无奈的说,我们无法得到一个$O(N)$的算法,这是因为并非所有的操作都能在$O(1)$时间内完成,均摊成本无法到达1,所以我们可以得到的结论是:
按秩合并并进行路径压缩的算法是最优的并查集算法。
这也就是说,这个算法已经无法再进行优化了。但是一个成分十分接近于$O(N)$的算法已经十分实用了,不是吗?
具体的成本分析需要较高的数学和概率统计基础,大家感兴趣可以自己搜索论文查看~~(简而言之就是我也不会~~
我能否添加删除操作?
诚然,数据结构中删除是一项十分基础的操作,然而遗憾的是,并没有任何人能发明既能兼顾删除操作又可以和本文所说的一些算法一样高效且简单的算法。换句话说,你可以使用无优化的树形结构来保存并实现删除操作,但是效率会大大降低。
6.例题
两道简单的模板题,提高题目可能之后会有提高专场,本文还是以基础为主~~~(总而言之就是我现在不会~~
HDU 1232 畅通工程
此题十分简单,首先输入的是联通的城市,之后查询几个城市是否联通,那就直接建立并查集,合并,并使用
connected(int p, int q)接口查询即可。HDU 1198 Farm Irrigation
这道题有点意思,大意就是说这个农场有11种地块,按照先右后下的顺序告诉你每一种地块,然后问你我最少需要灌溉几次才能全部覆盖。
第一眼看上去是一个二维的数组,实际上远没有这么麻烦,直接从左往右数然后按一维编号即可。
第二个难点是联通的转化,首先选择你喜欢的方法把一个地块分解为四个方向,然后从A到K分别给每个地块赋予性质即可,我是使用的位运算。之后对于每一个地块检查右侧和下侧地块,检查上下左右连通性即可,如果联通就合并,不连通就拉倒,最后返回一下联通分量个数即可。因为要遍历一遍数组,所以复杂度是$O(N^2)$。
7.引用
这篇文章的很多实现以及理论均来自《算法(第4版)》,P136~P149,对我帮助很大。
其次,路径压缩算法来自一篇CSDN博客并经过我简单修改,然而由于我看的时候离现在有点时间了,我也找不到了,暂且对原作者表示感谢吧。