kuangbin带你飞专题1-简单搜索

Ramen 收录于算法笔记

2017-11-18 约 3530 字预计阅读 8 分钟

这是kuangbin带你飞专题系列讲解&题解。

从青岛站回来后深感自己菜，然后开始按专题刷题。kuangbin大神的这一系列专题真的不错，写起来很练基础。同时，练习的时候写一篇题解也是很好的加深印象的方法。

老规矩，所有代码你都可以在我的Github答案仓库找到。

这一组专题会讲解一些基础知识点，然后是逐题题解。我个人的建议是先看题目，然后看算法解析，做题时再考虑题解。

Have fun.

这一期专题的vjudge位置：Click me!，我的答案位置：Click me!。

0x01 算法讲解

这一期的主要算法是深度优先搜索（Depth First Search，简称DFS）和深度优先搜索（Breath First Search，简称BFS）。

讲之前，考虑如下图：

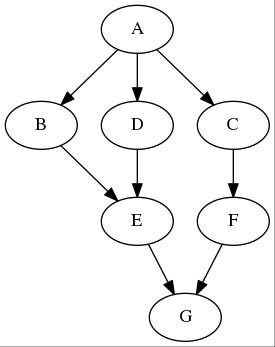
https://assets.lxdlam.com/img/1665505353_46872896.jpg — 图 1

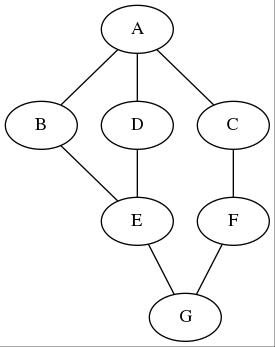
https://assets.lxdlam.com/img/1665505351_85d161d4.jpg — 图 2

可看出第一张为无向图，第二张为有向图。之后的讲解都将以这两张图为例子。

1.深度优先搜索

深度优先搜索，顾名思义，就是一条道走到黑的搜索，考虑图A，我们搜索时按照以下路径：

1
A -> B -> E -> G -> D -> C -> F

可以看出，我们的走法是走到头为止，每次当一个节点走到头，我们即回溯到第一个分叉点，从另一个出发。

下面针对第二张图举例：

1
A -> B -> E -> D -> G -> F -> C

这里要注意，无向图下优先级应根据实际问题定义。

从这里大家可以看出，深度优先搜索是基于栈的，也就是说，我们走到一个节点，把上一个节点入栈，继续往下搜索，直到搜索到末尾，出栈上一个节点，查看是否有其他路径，若有则继续搜索，没有就出栈再上一个节点，直到栈为空即搜索停止。在实际写代码过程中，由于函数调用是在栈上的，我们可以使用递归调用的方法来进行。所深度优先搜索是比较好写的。

深度优先搜索通常与回溯法合用，此时我们需要对状态进行标记。

这是一个通常的板子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
const int SIZE = 1e5 + 10;

int board[SIZE]; // ==> 数据域
bool vis[SIZE]; // ==> 标记是否到达过

void dfs(int i) {
    if(vis[i]) // ==> 访问过
        return;
  
    // 搜索操作...
  
    vis[i] = true; // ==> 标记已访问
    dfs(i + 1); // ==> 调整搜索方向
    // vis[i] = false; // ==> 回溯搜索
}

2.广度优先搜索

对于图A，搜索路径如下：

1
A -> B -> D -> C -> E -> F -> G

对于B：

1
A -> B -> D -> C -> E -> F -> G

这里看不出来什么，实际上就是按照层次去搜索，每次都搜索同一层次的。

这里看出，广度搜索是基于队列的，我们搜索都是把同层次入队，然后队顶出队搜索并重复上述过程直到队列为空。这里我们需要队列的配合，所以BFS也比DFS难写一点。

下面是一个比较常用的板子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <queue> // ==> 引入队列

const int SIZE = 1e5 + 10;

int board[SIZE]; // ==> 数据域
bool vis[SIZE]; // ==> 标记是否到达过

struct Node {
    int data; // ==> 数据域
    //... ==> 辅助信息域
}; // ==> 辅助节点，用于暂存信息

int bfs() {
    queue<Node> q;
    Node s; // ==> 起始节点
    Node t; // ==> 临时节点
    Node n; // ==> 变换用节点
  
    // 对s做一些操作...
    q.push(s);
    while(q.size()) {
        t = q.front();
        q.pop(); // ==> 出队
      
        n = t; 
        // 对n做一些操作
        if(vis[n.data])
            continue; // ==> n已到达过，跳过
        vis[n.data] = true; // ==> 标记n已到达
        q.push(n);
    }
}

当然，网上对这二者还有更好的讲解，大家最好参考其他的一起看，集思广益。

0x02 题解

注意，请先尝试自己做再看题解。本组题目链接为：Click me!。

题解

A. 棋盘问题 – POJ 1321

考点：DFS
难度：简单

最简单的DFS题，只是注意在搜索时，先进行一次层级遍历。也就是说：

1
dfs(row + 1, m);

这样就能在可放位置大于棋子数目的时候搜索较低层级。

B. Dungeon Master – POJ 2251

考点：BFS
难度：适中

可以说是一道标准的BFS题目，难度略微有一点大。主要本题是在三维迷宫中，这个能理清就很好做。注意移动方向只有6种，然后直接BFS即可。

C. Catch That Cow – POJ 3278

考点：BFS
难度：简单

比上一题简单很多倍的BFS。两个坑点：

退出条件时输出0，此时意味着John就和牛在一个位置
vis数组开$200000$，因为存在两倍传送操作，防止越界。

D. Fliptile – POJ 3279

考点：DFS、异或运算、枚举
难度：困难

[点灯游戏][1]。大概意思就是，你点击一个方块，会把周围方块全部状态翻转，游戏目的是把整个盘面都翻转过来。

本题要求输出解，多解情况下输出字典序最小的解。

这个题解法多种多样，其中最优的也是最难的解法是高斯消元法解$GF(2)$域上的异或方程组。这部分的研究我之后单独开一篇文章来讲，这里就讲最简单的DFS做法。

考虑其中一个块，假如这个块被翻转了两次，那说明这个块不应该被翻转。考虑任意一个块$A(i,j)$，假如这个块需要被翻转，能影响它的有哪些？上下左右四个方向。于是我们可以逐行处理，第一行全部翻转，然后是第二行……直到倒数第二行结束之后我们判断一下最后一行是否全部是$1$即可。

这个题思路和代码都来自《挑战程序设计竞赛》，这也是一本好书，可以看一看。

E. Find The Multiple – POJ 1426

考点：DFS，构造
难度：适中

被$digits(res)\le 100$的大小吓住了？要搞高精度？其实就是题目在蒙人。考虑6，有$1100\mod 6 = 0$，也就是说，$1100$也只是符合要求的解；而且这个题有Special Judge，所以构造合适的解就行。由于是01串，我们可以对这个数直接往下搜索，所以dfs的调用是：

1
2
dfs(x * 10, step + 1);
dfs(x * 10 + 1, step + 1);

另外要注意，这个数压根不会超过unsigned long long的范围，而unsigned long long大约能表示$0 -{10}^{19}$的范围，所以枚举19位即可。

F. Prime Path – POJ 3126

考点：BFS、质数表
难度：适中

首先打一个质数表，然后遵照以下两条规则变换：

每次仅变换一位，且保证新的数为质数
第一位范围为$1-9$，其他位范围为$0-9$

然后套BFS板子就能做。

G. Shuffle’m Up – POJ 3087

考点：模拟
难度：简单

十分简单的一道题目。图上解释的很清楚，$S_1$和$S_2$间隔放置得到$S_{12}$，这个$S_{12}$下半部分重新切割成$S_1$和$S_2$。循环$n$次，假如能得到目标盘面则输出$n$，否则输出$-1$。

手动模拟一下可以知道，这个序列是循环的，循环$length(S_{12})-2$次后有$S_1’=S_1$和$S_2’=S_2$。模拟计数即可。

H. Pots – POJ 3414

考点：BFS、路径记忆
难度：适中

难度并不大，就是一个标准的BFS搜索，难点在于记忆搜索路径。这里要利用好容器，注意到这个和顺序有关，是一种FIFO的顺序，可以使用队列。我用了vector。

I. Fire Game – FZU 2150

考点：两点BFS
难度：困难

BFS比较难的一种题型。题目的意思是，俩熊孩子点草丛，每块草丛会以$1$的速度扩散火势，问烧光所有草丛的最短时间。

这一题的难点在于，搜索是两个点同时进行的，我们如下考虑：一个点带来的贡献值只能是$step+1$或者$step$，那么最终的答案是最长路径的值。遍历一遍所有可以烧的点组，两两进行BFS然后求出最短时间。

这个题还需要特判一下，假如只有一块草坪，那么也是$0$的时间。

~~放火烧山，牢底坐穿！！！~~

J. Fire! – UVA 11624

考点：顺序BFS
难度：适中

这个题看似是两点BFS，实际简单得多。从题目中知道，火比人快，所以存下火的节点，然后火节点先入队，然后是人节点入队，顺着下去BFS即可。节点加个判断位，如果是人而且到达了任何边界点，直接输出答案即可。这里注意一下，一个是火的节点不止一个，题目里有提到；另一个，题目问的是逃出时间，到达边界后还需要$1s$才能逃出，所以答案是$step+1$。

~~好气啊，uDebug数据全过，只要交都吃WA，后面发现构造函数忘记写step的初始化了。~~

K. 迷宫问题 – POJ 3984

考点：BFS、路径记忆
难度：适中

B的思路 + H的记忆方法。不再多说。

L. Oil Deposits – HDU 1241

考点：DFS、更新域
难度：适中

很简单的DFS，数联通块即可。这里用的技巧是，遇到@计数加1，同时dfs下去，把所有直接连通的块全部置成*。

M. 非常可乐 – HDU 1495

考点：BFS
难度：适中

也是一个BFS板子题。这个题考虑一个问题，三个杯子都可以倒，我们倒的方向可以是$S \to A$，$S\to B$，$A\to S$，$A\to B$，$B\to S$，$B\to A$，那最终的退出条件应该是

$$S_{\text{remian}} = \frac{S}{2} = \max(A,B)_{\text{remain}}$$

也就是说，$S$这个大杯子和$A$、$B$中较大的一个杯子中各占一半的量。这里也提示我们剪枝，假如这个$S$是奇数，根本就不用计算，必定不能被平分。

另：这个题还有另外一个特别有意思的数论做法，参看这里。

N. Find a way – HDU 2612

考点：BFS
难度：困难

这题难度主要是剪枝。我们可以考虑根据I题思路，对所有KFC均进行一次BFS，从中求最短时间，但是这样就会得到一个大大的TLE。这题实际做法是我们对两人各遍历一次，假如到达KFC就存下时间，最终求累积和的最小值。这里我用了一个map。

啊，这个专题从开坑到现在做完中间过了好久啊。。。。。

简单搜索部分还是挺简单的_(:зゝ∠)_（突出首尾呼应

我不会告诉你们我第一眼看到BFS毫无思路，然后意识到我做过的都是DFS，没写过BFS……

下期见！

目录